
….jpg)

We will do so with the help of the Karnaugh mapping technique. The next step is to simplify the two expressions. The Boolean expressions for the two output variables are given in Equation below for the SUM output (S) and in above Equation for the CARRY output (Cout): These expressions are then simplified by using any of the simplification techniques described in the previous chapter.
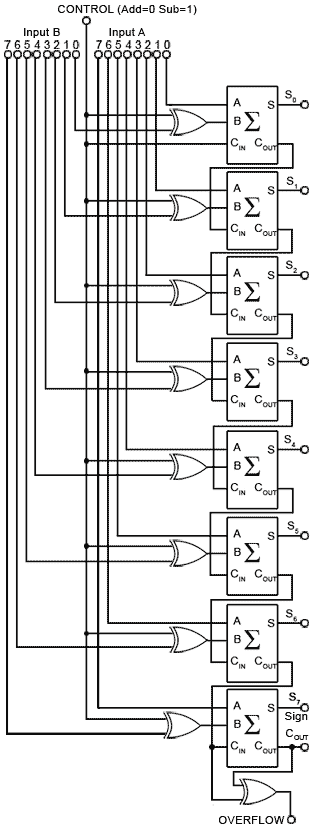
#Full adder subtractor circuit diagram full#
In order to arrive at the logic circuit for hardware implementation of a full adder, we will firstly write the Boolean expressions for the two output variables, that is, the SUM and CARRY outputs, in terms of input variables. A half-adder can be used for addition of LSBs only.įigure shows the truth table of a full adder circuit showing all possible input combinations and corresponding outputs. A full adder is therefore essential for the hardware implementation of an adder circuit capable of adding larger binary numbers. We have a similar situation for the other higher column bits. As a result, when we add the next adjacent higher column bits, we would be required to add three bits if there were a carry from the previous addition. We record the sum under the LSB column and take the carry, if any, forward to the next higher column bits. We begin with the addition of LSBs of the two numbers. Let us recall the procedure for adding larger binary numbers. The full adder circuit overcomes the limitation of the half-adder, which can be used to add two bits only. Such a building block becomes a necessity when it comes to adding binary numbers with a large number of bits. Full AdderĪ full adder circuit is an arithmetic circuit block that can be used to add three bits to produce a SUM and a CARRY output. 3.3, it could also be implemented by using an appropriate arrangement of either NAND or NOR gates.
However, these two expressions can certainly be represented in different forms using various laws and theorems of Boolean algebra to illustrate the flexibility that the designer has in hardware-implementing as simple a combinational function as that of a half-adder.Īlthough the simplest way to hardware-implement a half-adder would be to use a two-input EX-OR gate for the SUM output and a two-input AND gate for the CARRY output, as shown in Fig. While the first one representing the SUM output is that of an EX-OR gate, the second one representing the CARRY output is that of an AND gate. The Boolean expressions for the SUM and CARRY outputs are given by the equations belowĪn examination of the two expressions tells that there is no scope for further simplification. Figure 3.2 shows the truth table of a half-adder, showing all possible input combinations and the corresponding outputs. Such a circuit thus has two inputs that represent the two bits to be added and two outputs, with one producing the SUM output and the other producing the CARRY. A half-adder is an arithmetic circuit block that can be used to add two bits.


 0 kommentar(er)
0 kommentar(er)
